Performance Measures
![]()
Besides interpretability, predictive performance is the most important property of machine learning models. Here, I provide an overview of available performance measures and discuss under which circumstances they are appropriate.
Performance measures for regression
For regression, the most popular performance measures are R squared and the root mean squared error (RMSE). \(R^2\) has the advantage that it is typically in the interval \([0,1]\), which makes it more interpretable than the RMSE, whose value is on the scale of the outcome.
Performance measures for classification
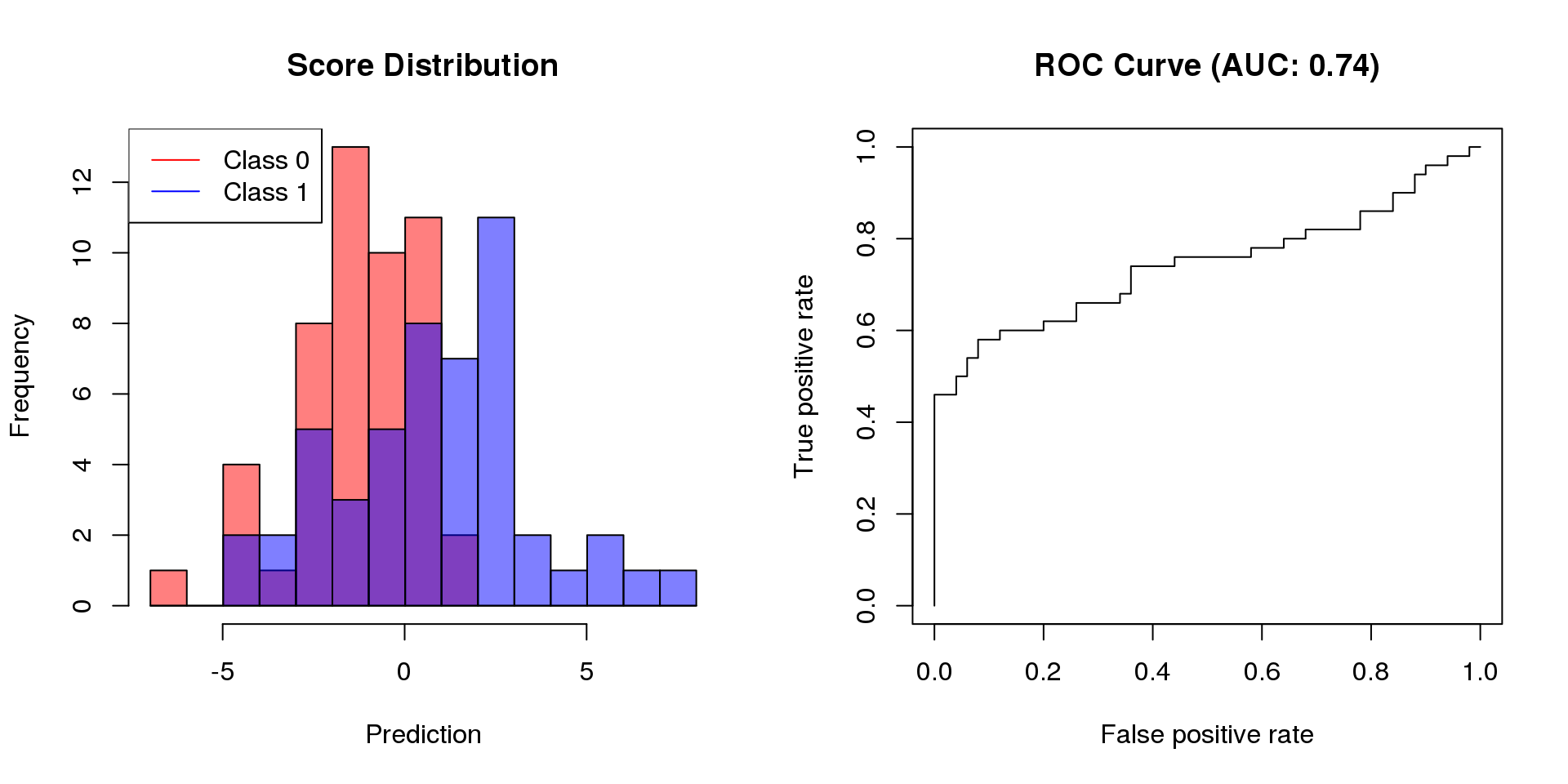
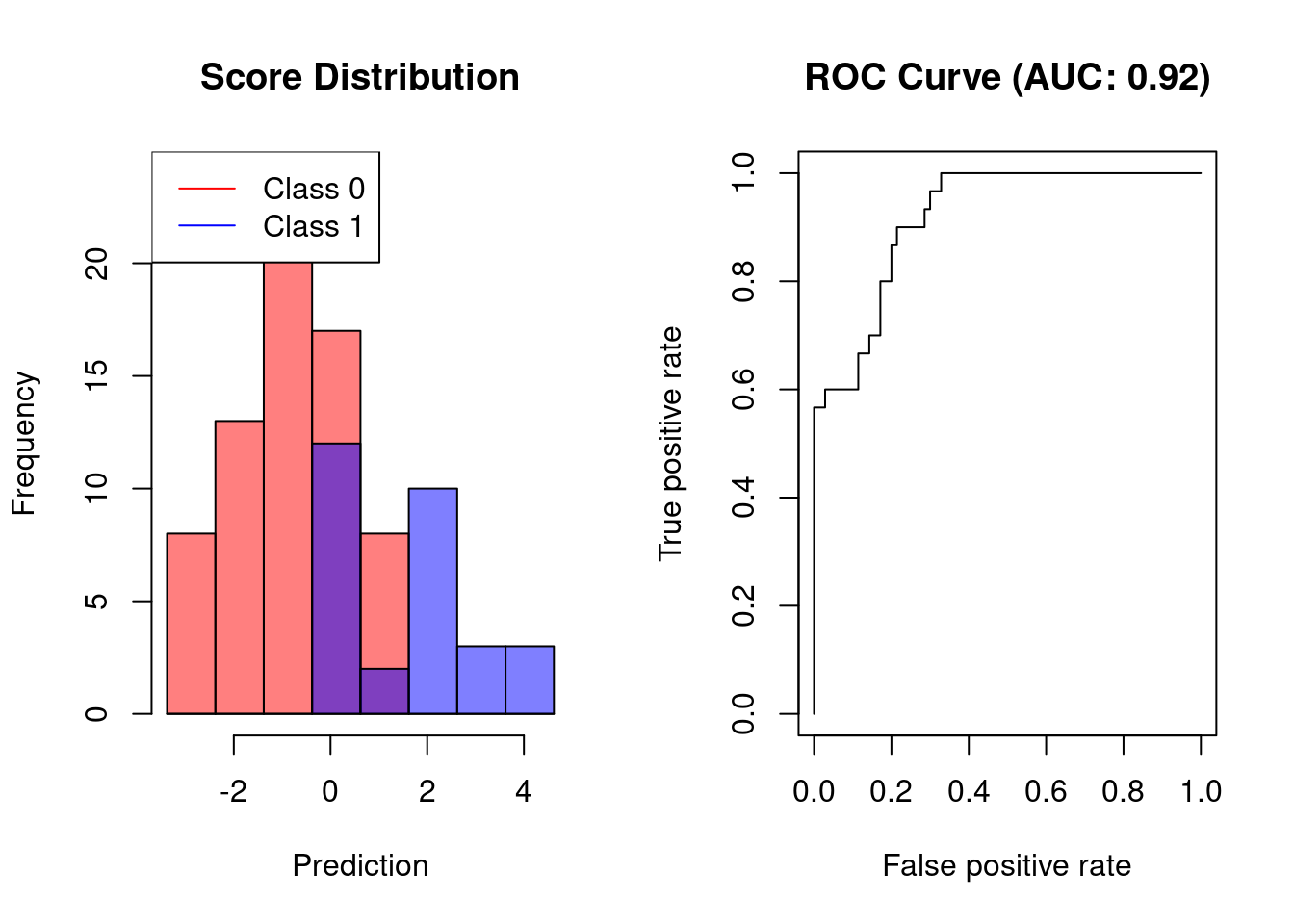
The performance of models for binary classification is evaluated on the basis of confusion matrices, which indicate true positives, false positives, true negatives, and false negatives. Based on these quantities, the performance measures of sensitivity and specificity (balanced accuracy) are derived. In specific circumstances, it is worthwhile to consider recall and precision (the F1 score) rather than sensitivity and specificity.
For scoring classifiers, the area under the receiver operating characterstic curve (AUC) can be used to measure the sensitivity-specificity tradeoff for different classification thresholds.
Performance measures for feature selection
When comparing models with different number of features, model complexity should be taken into account through measures such as the adjusted \(R^2\) or the Akaike information criterion (AIC). Alternatively, to curb overfitting, model performance can be determined on an independent test set (e.g. via cross validation).
Posts about performance measures
The following posts discuss performance leasures for supervised learning and how they can be computed using R.

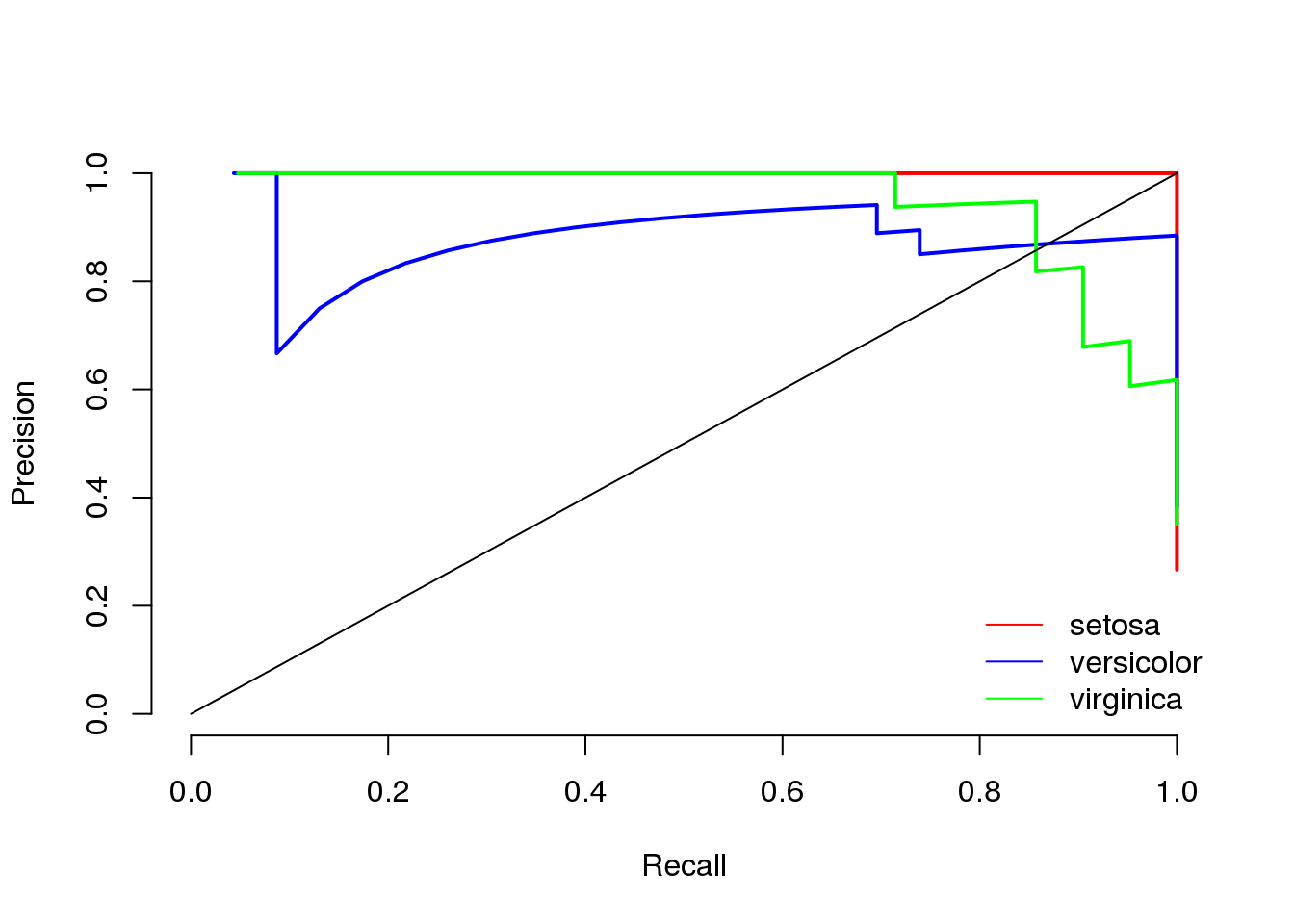
Performance Measures for Multi-Class Problems
Performance Measures for Feature Selection
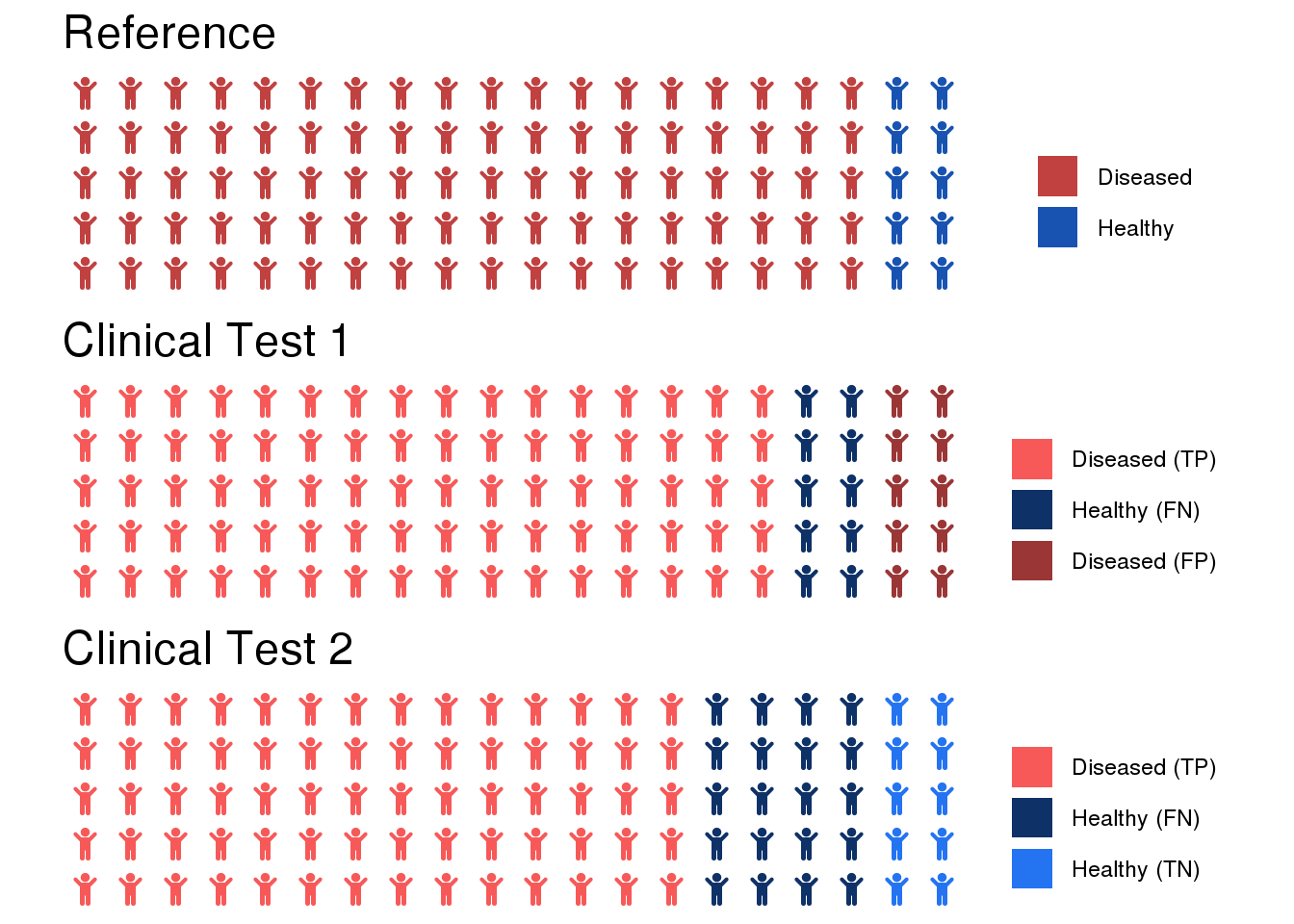
The Case Against Precision as a Model Selection Criterion