Parametric significance tests assume that the data follow a specific distribution (typically the normal distribution). If their assumptions are met, they have greater power than non-parametric test. Otherwise, non-parametric tests should be used. Thus, parametric tests should only be used after carefully evaluating whether the assumptions of the test are sufficiently fulfilled.
This table gives an overview of the most popular parametric tests:
| Test | Test for what? |
|---|---|
| Student’s t-test, Paired Student’s t-test | Difference in paired means and means |
| Chi-squared test | Independence of group counts |
| One-way ANOVA | Difference in means of several independent variables |
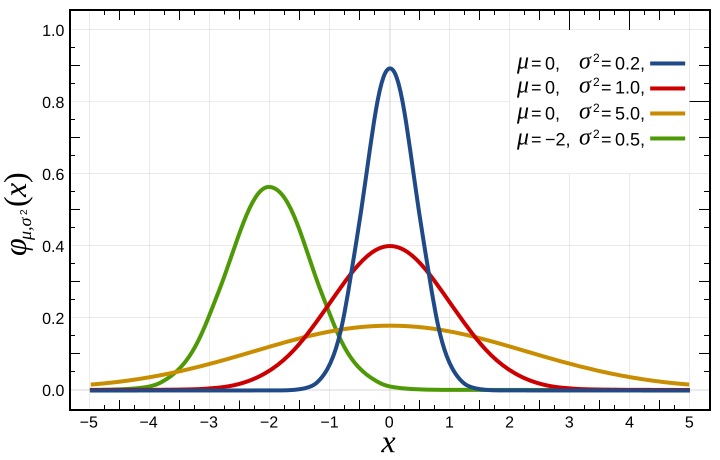
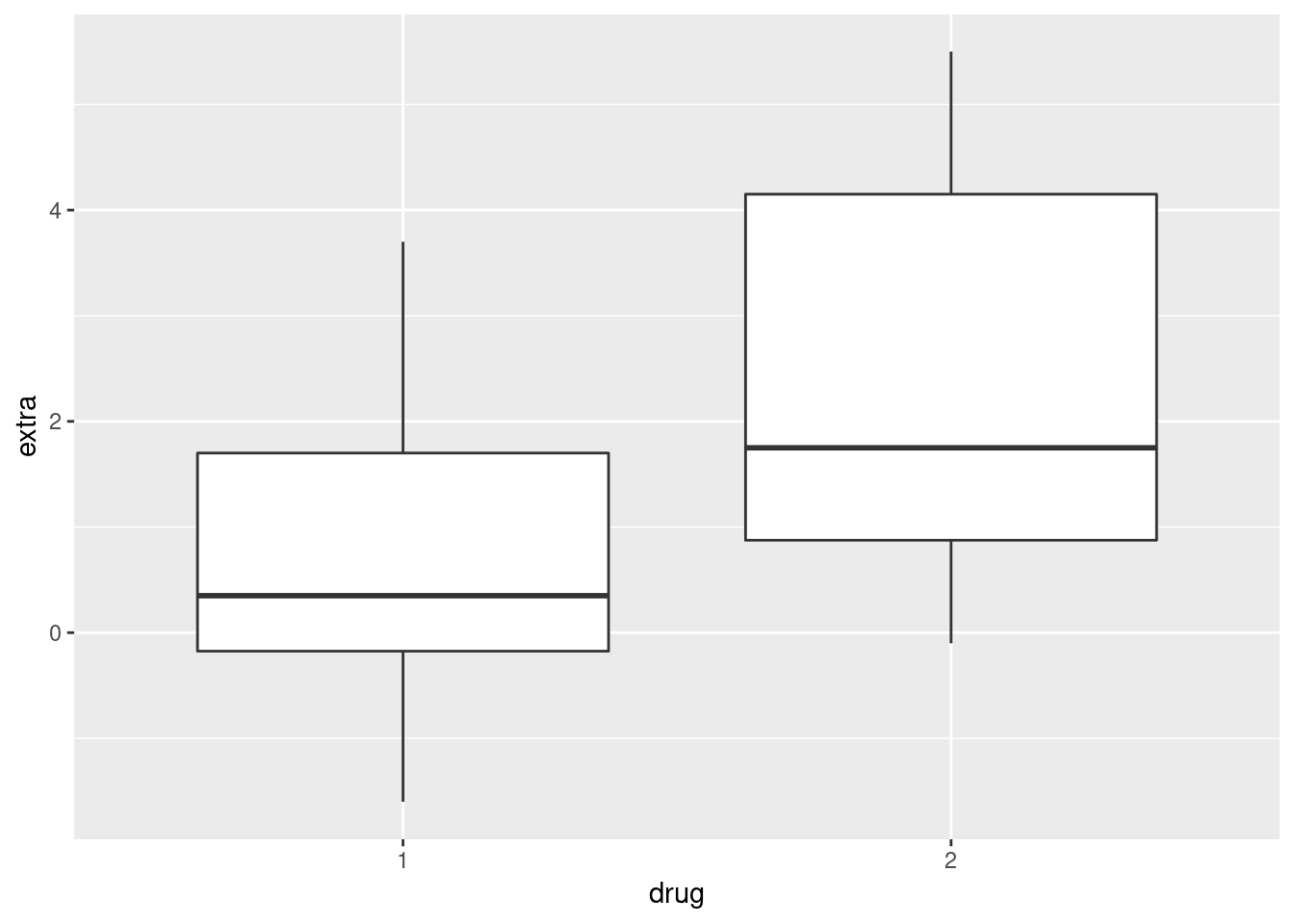
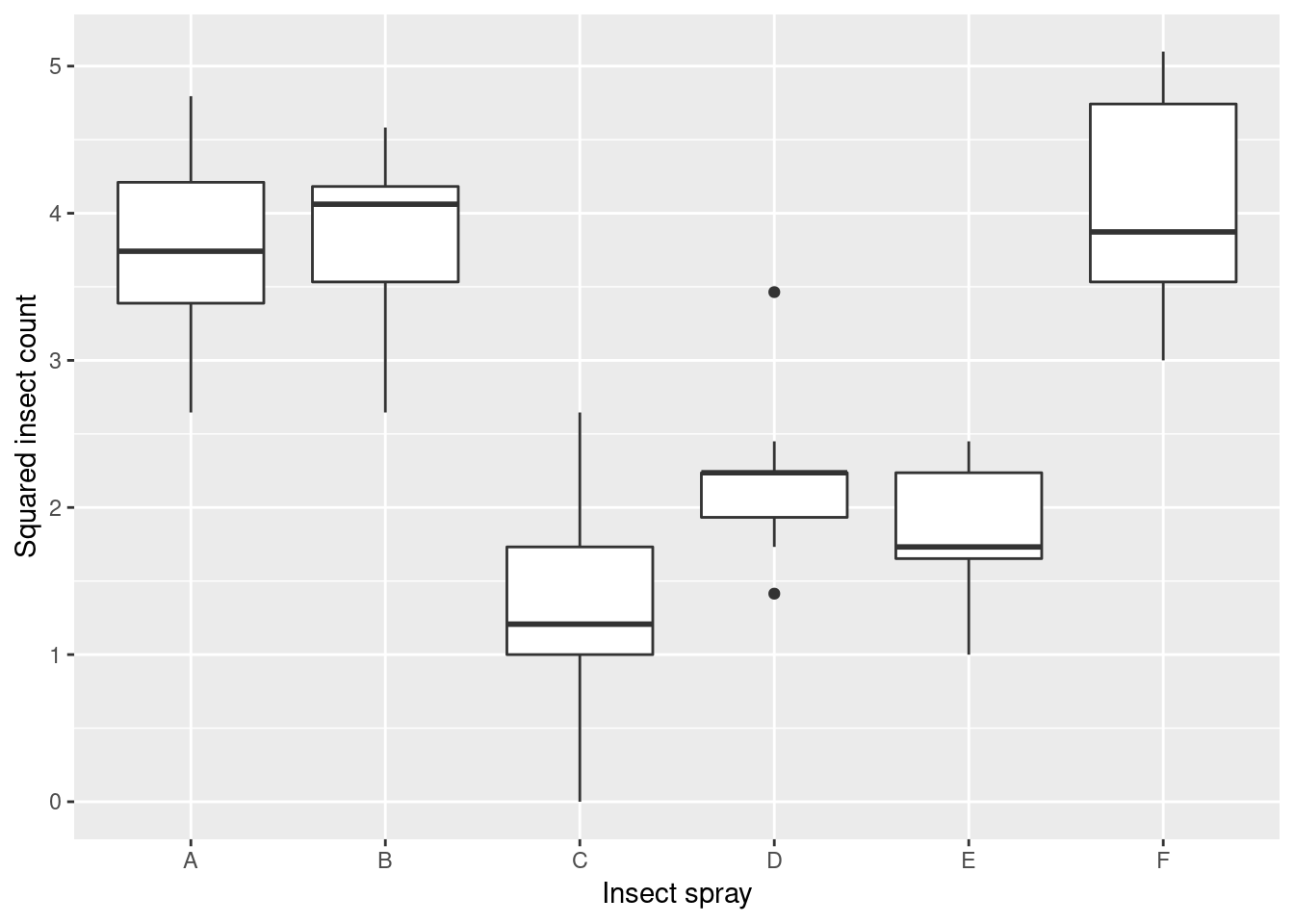
The means of quantitative measurements from two groups can be compared using Student’s t-test. To compare the means of measurements for more than two levels of a categorical variable, one-way ANOVA has to be used. Here, we’ll explore the parametric, one-way ANOVA test as well as the non-parametric version of the test, the Kruskal-Wallis test, which compares median values.
Parametric tests are subject to assumptions about the properties of the data. For example, Student’s t-test is a well-known parametric test that assumes that sample means have a normal distribution. Due to the central limit theorem, the test can be also applied to measurements that are not normally distributed if the sample size is sufficient. Here, we will investigate the approximate number of samples that are necessary for the t-test to be valid.
In this post, we will explore tests for comparing two groups of dependent (i.e. paired) quantitative data: the Wilcoxon signed rank test and the paired Student’s t-test. The critical difference between these tests is that the test from Wilcoxon is a non-parametric test, while the t-test is a parametric test. In the following, we will explore the ramifications of this difference.
