Bayesian methods make use of Bayes’ theorem to perform statistical inference. Bayes’ law states that a conditional probability can be decomposed in the following way:
\[P(A | B) = \frac{P(B|A) P(A)}{P(B)}\]
where \(A\) and \(B\) indicate two events. The following terms are assigned to each of the quantities:
\(P(A|B)\) is the posterior probability
\(P(B|A)\) is the likelihood of \(B\) given \(A\)
\(P(A)\) and \(P(B)\) are the marginal probabilities for \(A\) and \(B\), respectively
In statistical modeling, another parameterization is typically used. Let \(X\) indicate the data and \(\Theta\) indicate the model parameters. Then Bayes’ rule can be formulated as follows:
\(P(\Theta | X)\) is the posterior probability of the model given the data
\(P(X|\Theta)\) is the likelihood of the data given the model
\(P(\Theta)\) gives the prior probabilities for the model parameters
\(P(X)\) indicates the probability of the data
The proability of the data, \(P(X)\) can be ignored when we are interested in \(P(\Theta | X)\) merely for model selection since \(P(X)\) is independent of the model.
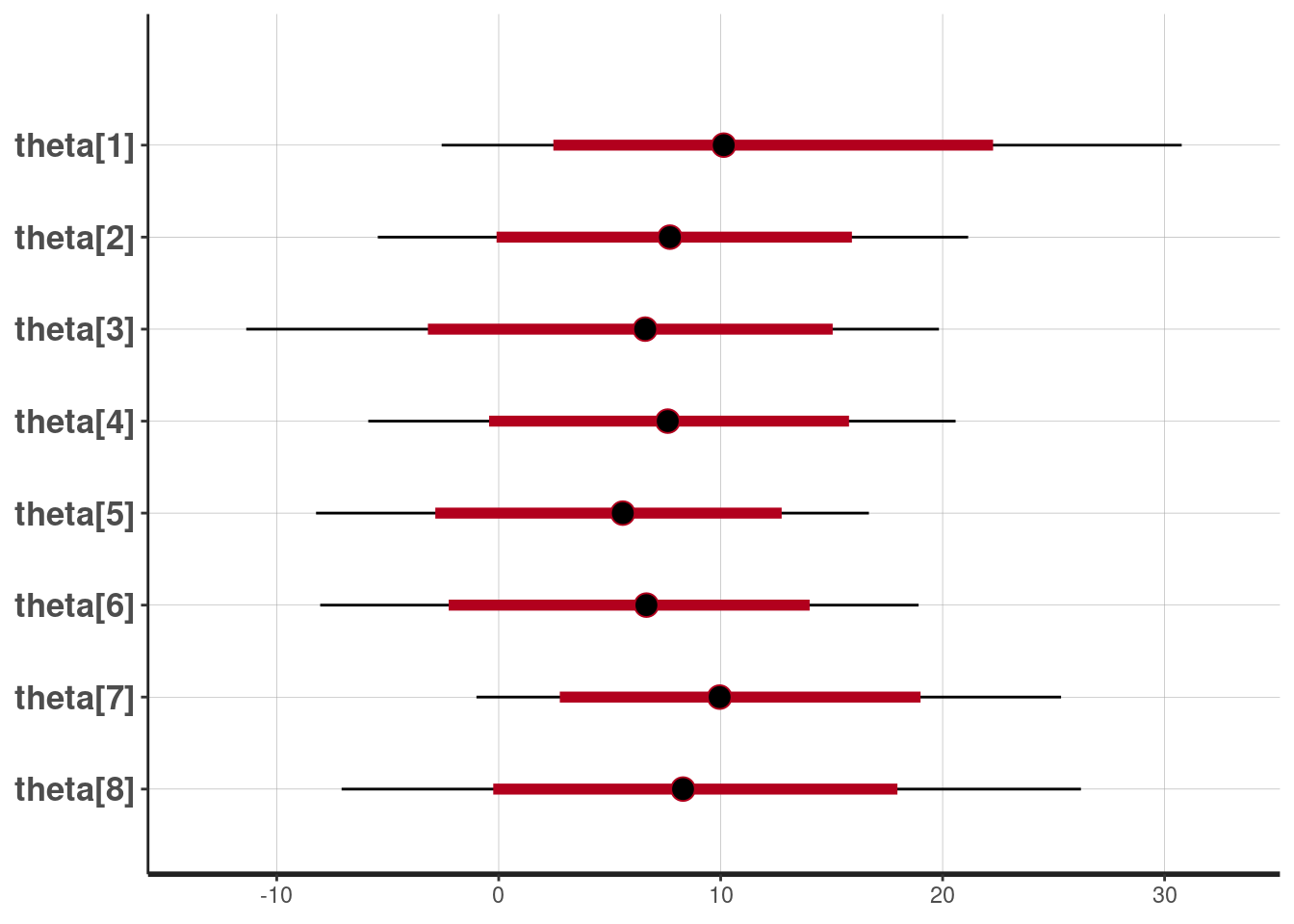
Due to the use of prior knowledge, Bayesian approaches are always parametric in the sense that these methods specify models based on assumptions about the data generation process. A challenge of Bayesian methods is that the posterior distribution may be very hard to compute explicitly, which is why Markov chain monte carlo (MCMC) is often used to sample from the posterior distribution.
Inference vs prediction
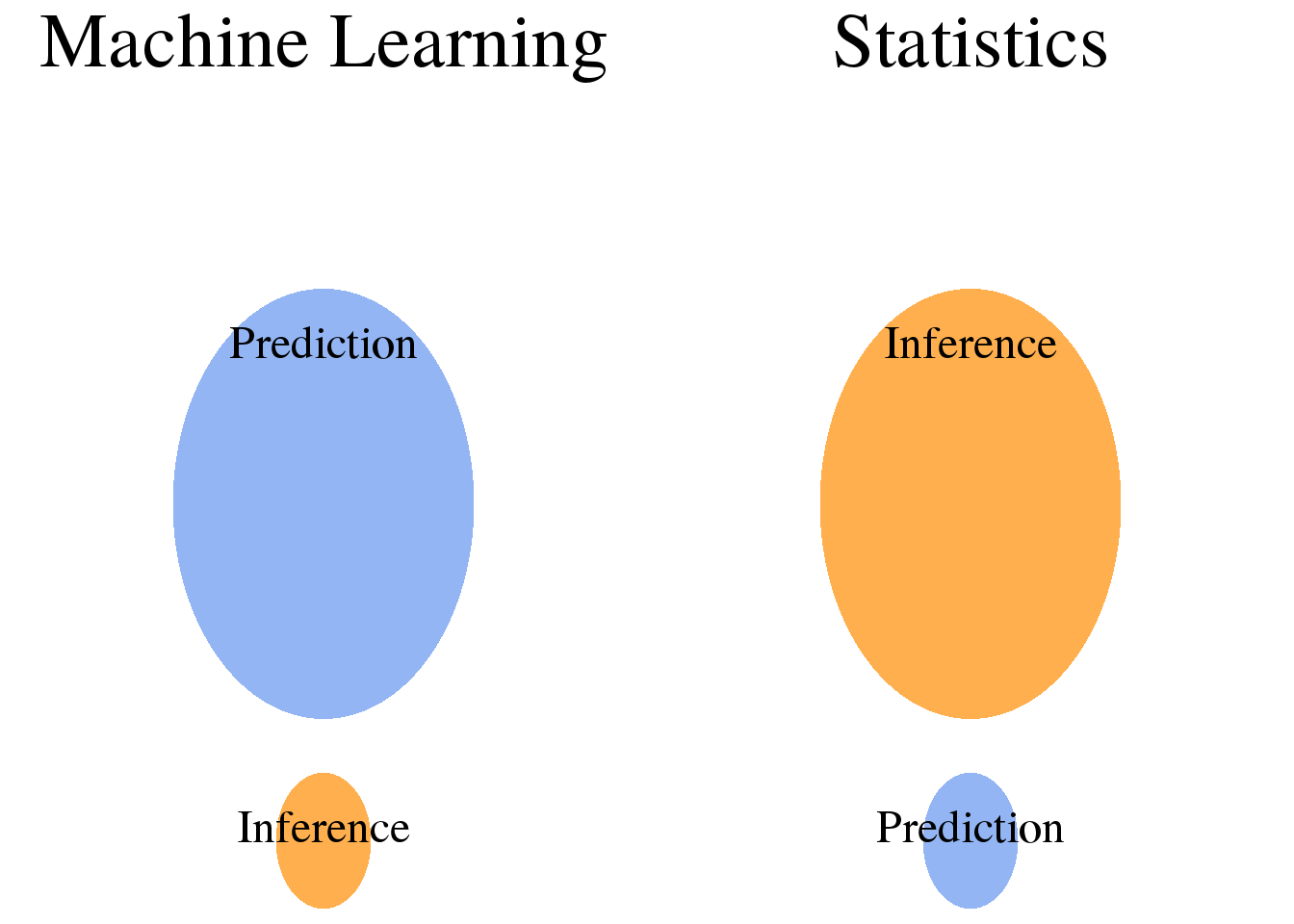
Bayesian methods are concerned with statistical inference rather than prediction. Inference is concerned with learning how the observed outcomes are generated as a function of the data. Prediction, on the other hand, is concerned with building a model that can estimate the outcome for unseen data. Note that there are methods that can be used for both tasks. For example, logistic regression can be used to measure the impact of individual features on the outcome (inference) and to estimate the outcome for new observations (prediction).
In essence, the difference between inference and prediction boils down to model interpretability. If a model is interpretable (i.e. you can understand how the predictions are formed) it probably performs inference, while models that are hard to interpret probably perform prediction. To make the distinction clearer, consider the following examples:
Inference methods: all Bayesian methods; to a certain extent some machine learning methods (e.g. linear regression or logistic regression)
Prediction methods: all machine learning models, particularly those that are non-parametric (e.g. decision trees, neural networks, or non-linear support vector machines)
The terms inference and prediction both describe tasks where we learn from data in a supervised manner in order to find a model that describes the relationship between the independent variables and the outcome. Inference and prediction, however, diverge when it comes to the use of the resulting model:
Inference: Use the model to learn about the data generation process. Prediction: Use the model to predict the outcomes for new data points.
Probabilistic programming enables us to implement statistical models without having to worry about the technical details. It is particularly useful for Bayesian models that are based on MCMC sampling. In this article, I investigate how Stan can be used through its implementation in R, RStan. This post is largely based on the GitHub documentation of Rstan and its vignette.
Introduction to Stan Stan is a C++ library for Bayesian inference.
